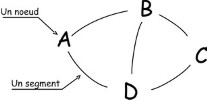
Un graphe est ensemble de noeuds reliés par des segments.
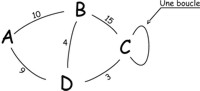
On peut donner une valeur pour chaque segment, on parle alors de graphe valué
un segment qui relie un noeud a lui même est une boucle
Introduction
Ce cours est une tentative de conserver ce qui m'a été enseigné en première année de l'IUP MIAGE de Nice...
il n'est pas terminé, peu étoffé et encore désagréable à lire (veuillez excuser les trop nombreuses
fautes d'orthographes, les paragraphes et les shémas manquant) ... Cependant, il a le mérite d'être écrit par un étudiant et d'être a la disposition
de tous.
Si vous trouvez des erreurs ou fautes et que vous avez du temps à lui consacrer, vous serez le (ou la) bienvenue
c'est ici...
Tout d'abord, un peu de vocabulaire : Recherche Opérationnelle, Mathématiques de la décision,
Techniques quantitatives de la gestion, programation dynamique... Voici quelque uns des termes
liés a ce dont traite ce cours, je choisi d'utiliser ''recherche opérationelle'' parcequ'il me plait...
Si on vous demande ce que ça veut dire, Voici une réponse simple : La recherche opérationnelle est l'application
de méthodes scientifiques dans la résolution de problèmes courants...
Quelques exemples :
Les problèmes d'affectation
L'exemple le plus courant est le problème de l'affectation de taches a des ouvriers. Chaque
ouvrier a des aptitudes et des spécialités différentes, on recherche une répartition des
taches qui soit optimale...
Si on se base sur un problème de petite taille, ont peut envisager de créer une liste
exhaustive de toutes les combinaisons possibles (pour 3 ouvriers et 3 taches, ont obtient 3!
c'est a dire 6 combinaisons possibles...
A une plus grande échelle, l'énumération des différentes combinaisons est impossible (Pour
25!, un ordinateur qui énumèrerait un millions de combinaisons par seconde mettrait
approximativement 25 milliards d'années...)
c'est pour ces cas de figure que la recherche opérationnelle propose des méthodes qui permettent
de construire une solution optimale, ce qui permet d'éviter l'énumération.
Les problèmes d'ordonnancement
L'exemple qui me vient a l'esprit est celui d'une construction, Pour mener a bien un chantier
chacun peut concevoir qu'il faut établir un ordre impératif pour les différentes tâche à accomplir
Imaginez que vous faites construire la maison de vos rêves, vous comprendrez facilement que la maçonnerie
et la charpente devront être terminées pour que le peintre commence sont travail...
Les bricoleurs savent qu'il n'et pas toujours facile d'organiser les petits travaux dans lesquels ils
se lancent, La recherche opérationnelle propose des méthodes systématiques qui permettent d'obtenir des
résultats optimaux... Bien entendu, l'intérêt de ces méthodes est qu'elle s'appliquent avec autant
d'efficacité sur les grands projets...
Les problèmes de flot
Les exemples courants sont l'écoulement de liquides dans des conduites, la capacité d'un réseaux de distribution électrique, ou encore le débit d'un réseau de voix routières ou ferroviaires...
Quelques bouquins de référence
Précis de recherche Opérationnelle : R. Faure, éditions DUNOD (1 volume de 3 chapitres)
Méthodes & modèles de la RO : A Kaufman, éditions DUNOD (3 volumes de 800 pages)
Exercices de RO : ROSEAUX, (c'est une équipe de profs), éditions MASSON (3 volumes)
La théorie des graphes
Cette partie présente de façon minimaliste la théorie des graphes... Bouquin de référence : Graphes & Hypergraphes...
On distingue 2 familles de graphe :
- Les graphes orientésPour info, la représentation graphique d'un graphe est appelé un diagrame sagittal...
- Les graphes non orientés
Graphe, graphe valué, boucle :
 |
Un graphe est ensemble de noeuds reliés par des segments. |
 |
On peut donner une valeur pour chaque segment, on parle alors de graphe valué |
Graphe simple (non orienté) :
Pour les graphes non orientés, on parle d'arrêtes & de chaînes...
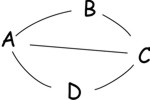 |
c'est un graphe simple (non orienté) |
Graphe orienté :
Pour les graphes orientés, on parle d'arcs, de chemins, ou de circuits
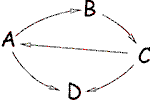 |
c'est un graphe orienté |
Graphe & composante Connexe
Soit X un noeud du graphe G. La composante connexe de X dans un graphe G est l'ensemble des sommets
pouvant être atteints à partir de X dans G.
Si X = G, le graphe est connexe...
Graphe fortement connexe...
Si G est un graphe orienté, il sera dit fortement connexe si pour tout couple de sommet (X,Y), il existe un chemin de X à Y.
Les algorithme de recherche de plus court chemin
Algorithme de Ford...
Son but est la recherche du plus court chemin entre 2 noeuds d'un graphe.
Quelques conventions
On note X0, X1, ... ,Xn les différents noeuds
Pour chacun d'entre eux, on crée une variable λ :
λ0, λ1, ... ,λn
Xj désigne l'extrémité de tout arc ayant pour origine Xi
(Xi,Xj) désigne la valuation de l'arc Xi,Xj
Déroulement de l'algorithme :
Initialisation :
λ0=0;
λi=+ ∞ quelquesoit i ≠ 0
On initialise λ0 à la valeur 0 puis et on donne à tout les autres λ la valeur
la plus grande possible...
Itérations :
Pour i de 0 à n :
Pour chaque Xj (j désigne l'extrémité de tout les arcs ayant Xi pour origine...) :Si λi + v(Xi,Xj) < λj, alorsλj <= λi + v(Xi,Xj) (λj prend la valeur de λi + v(Xi,Xj)...)Sinonne rien faire...
Condition d'arrêt :
On arêtte le déroulement si pour i de 0 à n, la relation (λi + v(Xi,Xj) < λj) n'a jamais été vraie...
quelques explications
l'idée utilisé est de parcourir tous les noeuds du graphe [X0, X1, ... ,Xn].
Pour chacun de ces noeuds, ou va parcourir les arcs qui en sont issus pour arriver au noeud succésseur
(les noeuds Xj).
On associe à ces Xj une valutation (λ0, λ1, ... ,λn)
en aditionant la valeur de l'arc et la valuation du noeud dont l'arc est issu
[λj <= λi + v(Xi,Xj)].
On recomence alors le parcours de tous les noeuds (X0, X1, ... ,Xn)
L'algorithme s'arette si on a parcouru tous les noeuds sans faire de modification dans les λn
Présentation du résultat :
La valeur du plus court chemin entre X1 et Xnest représentée par le dernier
Xn calculé.
Pour retrouver ce chemin, on va choisir les arcs en suivant la règle suivante :
- on calcule la différence λj - λi et on la compare à la
valuation de l'arc.
- Le plus court chemin est constitué par les arcs pour lesquels v(Xi,Xj) =
λj - λi
Essai sur un graphe de taille modeste...
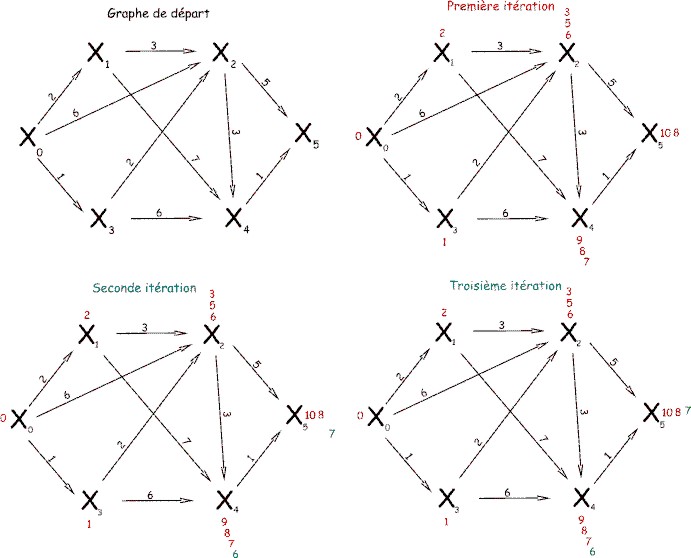 |
Comment on retrouve le résultat ??
λ5 - λ4 = 7 - 6 = 1 => on choisis l'arc X4, X5...
λ4 - λ2 = 6 - 3 = 3 => on choisis l'arc X2, X4...
λ2 - λ3 = 3 - 1 = 2 => on choisis l'arc X3, X2...
λ3 - λ1 = 1 - 0 = 1 => on choisis l'arc X0, X3...
et c'est terminé : Le chemin le plus court est donc X0, X3, X2, X4,
X5, sa valeur est 7.
Démonstration de la validité de cet algo...
Pour la démo, il va falloir attendre que j'ai un peu plus de temps...
Avantages & inconvénients ...
- l'algo de Ford est sensible à la numérotation (CF fonction ordinale)
- Il ne supporte pas les graphes comportant des circuits
Algorithme de Dantzig : En cours de frappe...
Voici l'algorithme :
Initialisations
μ0 = 0; A0 = {X0}; k = 0;
Itérations
Poser Bk = Ensemble des sommets de Ak ayant au moins 1 successeur hors de Ak
Pour chaque Xi ∈ Bk, parmi ses successeurs
Algorithme de Bellman
Cet algo est simple mais il pose 2 restrictions :
- Le graphe ne doit pas comporter de circuit.
- La numérotation doit suivre une fonction ordinale : quelquesoit Xi, Xj On a i < j
Comment construire une numérotation conforme ?
On dispose d'un algorithme :
Initialisations
k= 0;
Itérations
- Attribuer le numéro k+1 à un sommet sans prédécesseur ou a défaut a un sommet dont tous les
prédécesseurs ont étés numérotés...
- Incrémenter k et recommencer tant que tous les sommet ne sont pas numérotés.
Application :
Si on applique cet algo à notre graphe, on obtient la numérotation suivante :

|
Voici l'algorithme :
Comme l'algo de Ford, on se propose d'associer des valeurs λk aux sommets Xk, avec k allant de 0 à n...
Initialisations
Poser λ0 = 0 et k = 1;
Itérations
Pour k de 0 à n, poser :
λk = Minj {λj + v(Xj,Xk)}
(j représente tous les sommets prédécesseurs du sommet courant (Xk))
Application sur notre exemple :
λ0 = 0
calcul de λ1 : le sommet X1 n'a qu'un prédécesseur :
λ1 = λ0 + v(X0,X1) = 0 + 2 = 2
calcul de λ2 : le sommet X2 n'a qu'un prédécesseur :
λ2 = λ0 + v(X0,X2) = 0 + 1 = 1
calcul de λ3 : le sommet X3 a 3 prédécesseurs :
λ3 = λ1 + v(X1,X3) = 1 + 3 = 4
λ3 = λ0 + v(X0,X3) = 0 + 6 = 6
λ3 = λ2 + v(X2,X3) = 1 + 2 = 3
=> On choisit la valeur minimum : λ3 = 3
calcul de λ4 : le sommet X4 a 3 prédécesseurs :
λ4 = λ1 + v(X1,X4) = 2 + 7 = 9
λ4 = λ3 + v(X3,X4) = 3 + 6 = 6
=> On choisit la valeur minimum : λ4 = 6
λ4 = λ2 + v(X2,X4) = 1 + 6 = 7
calcul de λ5 : le sommet X5 a 2 prédécesseurs :
λ5 = λ3 + v(X3,X5) = 3 + 5 = 8
λ5 = λ4 + v(X4,X5) = 6 + 1 = 7
=> On choisit la valeur minimum : λ5 = 7
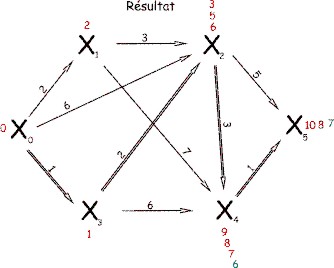
Comment trouver le chemin minimal :
- La valeur du chemin minimal est la dernière valeur calculée
- Pour retrouver le chemin, on remonte dans la trace de l'algorithme : pour notre exemple,
λ5 est issu de λ4, λ4 est issu de
λ3, λ3 est issu de λ2 qui est lui même
issu de λ2.
Le chemin minimal est donc : X0, X2, X3, X4, X5
pour une valeur de 7.
Retrouver les niveaux dans un graphe
Dans un graphe sans circuit, on peut trouver des niveaux successifs de la façon suivante :
- Ce sont des ensembles consécutifs de sommets.
- On appellera niveaux 0 l'ensemble des sommets sans prédécesseur.
- Le niveau n est constitué des sommets sans prédécesseur après suppression du niveaux n-1.
Voici un algorithme :
Cet algorithme est basé sur la liste des prédécesseurs. (c'est une liste des sommet du graphe ou on associe a chaque sommet la liste de ces prédécesseurs...)
Initialisation :
n = 0;
Créer la liste des prédécesseur;
Itérations :
tant que tous les sommets ne sont pas marqués, faire :
- On marque dans la liste tout sommet sans prédécesseur, ce sera les sommets de niveau n
- On Supprime tous les sommets marqués
- on incrémente n
Voici un Exemple :

|
Table des prédécesseurs :
| Sommet | Prédécesseurs |
| A | |
| B | A |
| C | A |
| D | BCA |
| E | DBC |
| F | ED |
| G | E |
| H | EF |
| I | EF |
| J | EHI |
Le concept de réseaux de transport
Un réseau de transport est un graphe qui a les propriétés suivantes :
- il est orienté, connexe, valué et sans boucle.
- 1 seul de ces sommet n'a pas de prédécesseurs : c'est la source.
- 1 seul de ces sommet n'a pas de successeurs : c'est le puit.
- La valuation des arcs de ce graphe est appéllée la capacité (α), elle est positive.
Le flot (Φ) dans un réseau de transport
c'est une seconde valuation qui répond a 2 règles :
- Φ(i,j) <= α(i,j) quelquesoit i,j
(le flot de l'arc i,j est inférieur ou égal à la capacité de cet arc quelquesoit i et j)
(le flot entrant est égal au flot sortant quelquesoit le noeud (sauf pour la source et le puit...))
Quelques définitions
La coupe :
C’est une partition d’un réseau telle que P contienne la source (noté a) et P contienne le puit (noté z).
Capacité d’une coupe :
C’est la somme de tous les arcs dont l’origine se trouve dans P et l’extrémité dans P barre
Algorithme de Ford & Fulkerson
Cet algorithme se propose d'améliorer le flot dans un réseau de transport. Chaque
itération se compose de 2 phases :
- On crée une liste des sommets marqués du réseau. Cette liste représente
un chemin pour atteindre le puit en partant de la source.
- Cette liste est utilisée pour mettre a jour le flot du réseau de transport.
conventions pour la notation :

|
Algorithme :
Initialisation :
Φ(x,y) = 0;
On associe à chaque arc un flot nul.
v(Φ) = 0;
Le flot dans le réseau est alors nul lui aussi.
Itérations : étape 1
Poser a(-,∞);
Ajouter des sommets dans cette liste en respectant les règles suivantes :
- Le nouveau sommet (y) doit être relié par un arc à un sommet (x) déjà marqué au cours de l'itération.
- Le coefficient Δy doit être non nul, on le calcule de la façon suivante :
- Si y est successeur de x :
- Δy = MIN [ Δx , α(xy) - Φ(xy) ]
- On marque le sommet (X+ , Δy)
- Si y est le prédécesseur de x :
- Δy = MIN [ Δx , Φ(xy) ]
- On marque le sommet (X- , Δy)
Itérations : étape 2
si on a terminé l'étape 1, 2 cas sont possibles :
- Soit on a pu marqué le puit :- On va faire une mise a jour des Φ(x,y) :- Soit on n'a marqué tous les sommets possibles et on ne peut pas atteindre le puis (c'est la condition d'arrêt) : le travail est terminé.- Φ(x,y)nouveau = Φ(x,y)ancien +/- Δz.- puis recommencer à l'étape 1. (on crée une nouvelle liste...)
(on ajoute ou retranche Δz selon le signe de l'exposant dans la liste)
- On change les Φ(x,y) en "remontant" le chemin indiqué par la liste depuis le puit vers la source.
Comment vérifier le résultat :
on construit une coupe en utilisant d'un coté la dernière liste construite, de l'autre le reste des noeuds du réseau. La valeur de cette coupe doit être égale au flot maximum.

|
Quelques remarques :
Quand on fait un exo sur cet algo, la tentation est grande de s'arrêter en croyant a voir fini :
Il ,n'y a que 2 bonnes raisons pour s'arrêter :
- Il est impossible de marquer le puit...
- Tous les arcs issus de la source, ou tous ceux qui vont vers le puits, sont saturés.
Lors de l'initialisation, on vous propose de mettre tous les &Phi(x,y) = 0. On peut gagner pas mal
de temps en essayant de saturer "a la main" le réseau de transport : il y a 2 pièges a éviter :
- il faut faire attention à vérifier la loi de conservation du flot...
- Cette opération doit vous prendre 1 minute : ne vous cassez pas la tête, l'algo est la pour valider ou améliorer votre choix...
Algorithme de Roy
On a remarqué qu’il y a souvent plusieurs répartitions ayant un flot maximal. L’algorithme de Roy se propose de choisir parmi ces solutions une (ou plusieurs) répartition ayant un coût minimal.
Pour introduire cette notion, on ajoute une seconde valeur sur chacun des arcs : Le coût
Quelques définitions
Graphe antisymétrique :
Un graphe est antisymétrique si quel que soit l’arc arc (xy) il n’existe pas d’arc (yx),
Si un graphe n’est pas antisymétrique, ont peut le modifier pour qu’il le devienne, il suffit d’ajouter un sommet fictif et de répartir le coût sur les 2 arcs créés
Graphe d’écart :
Soit G 1 graphe antisymétrique avec un flot , on construit GE en suivant la recette suivante :
GE à les mêmes sommets que G.
Pour chaque arc xy de G :
- Si xy est non saturé dans G (α > Φ), on crée dans GE un arc xy de capacité αE(xy) = α(xy) –(xy).
- Sinon (xy est saturé), on ne crée pas d’arc dans GE
- Si le flot Φ(xy) ≠ 0, on crée dans GE un arc YX dont la capacité est :
αE(yx) = α(yx) - Φ(xy).- Sinon, on ne crée pas d’arc yx dans GE
Un dessin vaut mieux que de long discours :

|
Algorithme de Tabourier
Quelques définitions
Sommet saturé :
Soit x un sommet de X, x sera dit couplé par W s’il existe un sommet y tels que (xy) appartienne a W. On dira alors que x est saturé par y
De même, Soit y un sommet de Y, y sera dit couplé par W s’il existe un sommet x tel que (yx) appartienne a W. On dira alors qu’y est saturé par x
Sommet insaturé :
Un sommet est insaturé s’il n’est pas saturé
Chaîne alternée :
C’est une suite d’arrêtes prises alternativement dans W et hors de W. Chaque arrête ayant une extrémité commune avec l’arrête précédente et l’arrête suivante.
Chaîne alternée saturante (CAS) :
μ = (α1 , α2 , α3 , ... , αn) est une Chaîne Alternée Saturante si et seulement si :
α1 appartient à W
αn appartient à W
le sommet de classe X de α1 est insaturé
le sommet de classe Y de αn est insaturé
Chaîne alternée tronquée :
μ = (α1 , α2 , α3 , ... , αn) est une Chaîne Alternée Tronquée si et seulement si :
α1 appartient à W
αn n'appartient pas à W
le sommet de classe X de α1 est insaturé
Longueur d’une arrête :
L(xy) = - v(xy) si xy appartient à W sinon, L(xy)= v(xy)
Longueur d’une chaîne alternée :
Soit μ = (α1 , α2 , α3 , ... , αn)
une Chaîne alternée, alors :
![]()
Inversion de chaîne
alors là, il me manque un bout de cours...Présentation de l’algorithme :
Il se décompose en une phase préliminaire et une autre itérative :
Phase A : travail préliminaire
Le but est de construire un couplage minimal :
On parcourt chaque ligne dans l’ordre croissant des indices.
On repère le terme minimal dans la ligne.
Si ce terme n’est pas déjà couplé en Y (dans une colonne contenant déjà un terme marqué),
on le marque.
Le couplage ainsi obtenu est appelé W0
Phase B : algorithme
Nous allons numéroter les n lignes non marquées, ont les parcours dans l’ordre croissant des indices et ont leur affecte un numéro du type Xji(ou i va de 1 à n).
Pour i allant de de 1 à n : on va effectuer les 2 opérations suivantes
rechercher dans G muni de Wi-1 une CAS (ou a défaut une CAT) de longueur minimale ayant pour origine un γji dont xji est le sommet de classe X.
inverser cette chaîne alternée et appeler Wi le couplage ainsi obtenu.
Quelques remarques